No post anterior, falamos da necessidade de utilizar vários valores iniciais no algoritmo EM para verificar se a convergência se dá na mesma região. Hoje vamos programar este teste.
Para fazer isso, vamos fazer algumas alterações no código anterior:
- Nossa função vai receber o argumento adicional dif_parada, que é o critério de parada do algoritmo (ou a diferença máxima permitida entre duas estimações).
- Vamos criar uma variável para identificar se o algoritmo parou porque convergiu (ou seja, a diferença entre duas estimações consecutivas foi menor que dif_parada) ou se atingiu o limite máximo de iterações.
- Em cada um dos dois casos, uma mensagem deve ser exibida para o usuário.
algoritmoEM_tStudent = function(par_ini,max_ite,y,nu,plot.trace=0,dif_parada=10^-4){
theta.curr = c(par_ini[1],par_ini[2]);
n = length(y);
theta.trace = matrix(ncol=2,nrow=1);
theta.trace[1,] = theta.curr;
atingiu_maxit = TRUE;
for(i in 1:max_ite){
#Passo 1 do EM - calcular E(U|Y)
alfa = 0.5*(n + nu)
beta = 0.5*(nu + sum((y-theta.curr[1])^2)/theta.curr[2]);
u.y = alfa/beta;
#Passo 2 do EM - Maximizar a função Q
# em relação aos parâmetros
mu.hat = sum(y)/n;
sigma2.hat = u.y*(sum((y-mu.hat)^2)/n);
theta.curr = c(mu.hat,sigma2.hat);
theta.trace = rbind(theta.trace,theta.curr);
dif = abs(theta.trace[i+1,]-theta.trace[i,])
if(dif[1]< dif_parada & dif[2]< dif_parada) {
cat("Algoritmo convergiu com",i,"iterações.\n")
atingiu_maxit=FALSE;
break;
}
}
if(atingiu_maxit==T) cat("Algoritmo atingiu número máximo de iterações.\n")
if(plot.trace==1){
par(mfrow=c(1,2))
plot(theta.trace[,1],main=expression(mu),ylab='',
xlab='Iteração',type='l',lwd=2)
plot(theta.trace[,2],main=expression(sigma^2),ylab='',
xlab='Iteração',type='l',lwd=2)
}
return(theta.trace)
}
Antes o programa parava a execução depois que todas as iterações fossem executadas. Agora, se o algoritmo convergir antes, paramos sua execução e ganhamos tempo computacional e memória. Ou seja, estamos evitando realizar trabalho desnecessário.
Para testar se o algoritmo está convergindo para uma única determinada região, precisamos executá-lo a partir de vários valores iniciais. Porém, fazer cada um na mão pode ser trabalhoso, então vamos automatizar esse processo.
Primeiro, vamos criar um vetor de valores iniciais para os parâmetros $\mu$ e $\sigma^2$.
vi_mu = c(-2,-1,0,1,2)
vi_sigma2 = c(0.1,0.5,1,2,5)
Para cada par de valor inicial $(\mu^{(0)},\sigma^{2(0)})$, vamos executar nosso algoritmo e retornar a estimação dos parâmetros. Para armazenar os resultados da estimação, utilizaremos uma lista.
erro_max = 10^-4;
max_ite = 100;
result = list();
for(i in 1:length(vi_mu)){
result[[i]] = algoritmoEM_tStudent(c(vi_mu[i],vi_sigma2[i]),max_ite,y,nu,0,erro_max)
}
No código acima:
- Definimos o critério de parada como $10^4$.
- Definimos o número máximo de iterações igual a 100.
- Definimos a estrutura de dados que vai receber os resultados: a lista result.
- Para cada par de valores iniciais, executamos o algoritmo EM e armazenamos seu respectivo resultado em result.
Se executarmos o código, result será uma lista de tamanho 5 contendo os resultados da estimação de cada par de valores iniciais dos parâmetros.
> result = list();
> for(i in 1:length(vi_mu)){
+ result[[i]] = algoritmoEM_tStudent(c(vi_mu[i],vi_sigma2[i]),max_ite,y,nu,0,erro_max)
+ }
Algoritmo atingiu número máximo de iterações.
Algoritmo atingiu número máximo de iterações.
Algoritmo convergiu com 99 iterações.
Algoritmo convergiu com 91 iterações.
Algoritmo convergiu com 77 iterações.
> length(result)
[1] 5
Observe que o algoritmo atingiu o número máximo de iterações em 2 pares e convergiu antes para os restantes. Isso exemplifica que, dependendo do valor inicial, a convergência pode ser mais lenta, principalmente se os valores iniciais estiverem distantes da região de convergência.
Agora, precisamos analisar se a convergência se dá na mesma região. Para isso, vamos plotar as linhas de trajetórias das cinco estimações em um único gráfico. Para obtermos um bom gráfico, necessitamos de duas coisas:
- calcular os valores mínimo e máximo de estimações (caso contrário, algumas curvas podem aparecer parcialmente se o eixo y não for bem definido),
- identificar o número máximo de iterações dos resultados para definir até onde plotar a curva no eixo x.
Vejamos:
#encontrar os limites do eixo y para ambos parametros
#e o número máximo de iterações executado
min_mu = max_mu = min_sigma2 = max_sigma2 = NULL;
ite_res = NULL;
for(i in 1:length(result)){
min_mu = min(min_mu,result[[i]][,1]);
max_mu = max(max_mu,result[[i]][,1]);
min_sigma2 = min(min_sigma2,result[[i]][,2]);
max_sigma2 = max(max_sigma2,result[[i]][,2]);
ite_res = max(ite_res,dim(result[[i]])[1]);
}
O que estamos fazendo no código acima é varrer cada matriz de result, identificando os valores máximo e mínimo das estimações dos parâmetros. Se executarmos o código acima, obtemos
> cbind(min_mu,max_mu);
min_mu max_mu
[1,] -2 2
> cbind(min_sigma2,max_sigma2);
min_sigma2 max_sigma2
[1,] 0.01044391 5
> ite_res
[1] 101
Obtemos ite_res igual a 101 porque são 100 iterações do algoritmo mais a linha do valor inicial. Agora estamos prontos para construir o gráfico de trajetórias.
par(mfrow=c(2,1))
#Grafico para mu
plot(result[[1]][,1],type='l',main=expression(mu),
ylab='',xlab='Iteração',lwd=1,
xlim=c(0,ite_res),ylim=c(min_mu,max_mu))
abline(h=mu,col='blue',lwd=2)
abline(h=emv_mu,col='red',lwd=2)
for(i in 2:length(result)) lines(result[[i]][,1],lwd=1)
#Grafico para sigma2
plot(result[[1]][,2],type='l',main=expression(sigma^2),
ylab='',xlab='Iteração',lwd=1,
xlim=c(0,ite_res),ylim=c(min_sigma2,max_sigma2))
abline(h=sigma2,col='blue',lwd=2)
abline(h=emv_sigma2,col='red',lwd=2)
for(i in 2:length(result)) lines(result[[i]][,2],lwd=1)
Vejamos o resultado:
A linha azul representa o valor verdadeiro do parâmetro e a linha vermelha, o valor de seu EMV. Como a estimação de $\mu$ converge depois de uma iteração (discutimos isso no post anterior), nesse gráfico fica ruim de observar a convergência. Vamos alterar a janela do eixo x para xlim=c(0,5), apenas para observarmos o comportamento da saída do valor inicial para a estimação. No gráfico de $\sigma^2$ é mais fácil visualizar que o algoritmo está convergindo para o mesmo lugar (o EMV).
E se quisermos rodar o algoritmo para 20 valores iniciais? Ou 100? Seria bom gerar valores iniciais ao invés de escrevê-los a mão, concorda comigo? É o que fazemos abaixo:
set.seed(7)
vi_mu = rnorm(20,mean=0,sd=2)
vi_sigma2 = rgamma(20,shape=2,rate=2)
Dessa forma, geramos 20 valores iniciais para os parâmetros. Veja que para $\sigma^2$ estamos gerando de uma distribuição Gama, uma vez que seu valor deve ser positivo. Poderíamos utilizar outras distribuições? Claro que sim.
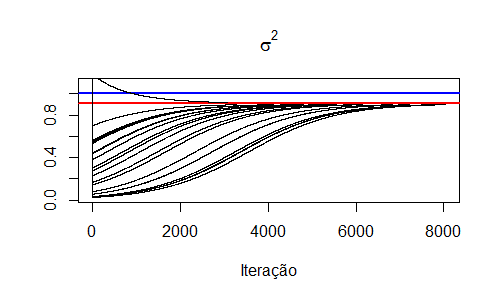
Alterei o limite máximo do eixo y do gráfico de $\sigma^2$ apenas para termos uma melhor visualização das curvas. Analisemos o gráfico acima:
- No gráfico de $\mu$, observamos a convergência para o mesmo ponto (EMV) após 1 iteração do algoritmo.
- No gráfico de $\sigma^2$, notamos que a convergência para a mesma região (EMV) partindo dos diferentes valores iniciais. Observe que há curvas que não alcançaram o EMV. Isso ocorre porque o algoritmo atingiu o limite de iterações que definimos.
Já analisamos o efeito do número de iterações máxima no resultado do algoritmo. Agora, qual o efeito de alterar o critério de parada do algoritmo? Ou seja, o que acontece se alteramos o critério que definimos para considerar convergência? Vamos fazer o teste com o valor de erro_max igual a $10^5$. O resultado é o "mesmo" que o anterior, pois as estimativas são as mesmas. A diferença é que o algoritmo demorou mais para convergir, ou seja, precisou de mais iterações para conferir o critério de convergência. No caso, obtemos um número máximo de iterações executadas igual a 230.
Por fim, faremos o mesmo exemplo, mas com um tamanho de amostra igual a 5 mil (utilize a mesma semente do exemplo anterior). Nesse caso, os valores do EMV dos parâmetros são mais próximos do valor verdadeiro (pois temos mais informação).
> emv_mu
[1] 0.003103879
> emv_sigma2
[1] 0.9086786
Executando nossa função para os 20 valores iniciais, 10 mil iterações e erro igual a $10^5$, obtemos o seguinte gráfico de trajetória para $\sigma^2$.
A partir do critério de parada estabelecido, o algoritmo convergiu antes de 10 mil iterações para todas as 20 execuções. Note que precisamos de muito mais iterações com essa amostra. Isso ilustra a necessidade de adequar o erro e o número máximo de iterações para cada problema que se tem em mãos. A análise gráfica ajuda muito nessa etapa.
Espero que tenha gostado da aula.
Até a próxima aula!





Nenhum comentário:
Postar um comentário