No último post implementamos um algoritmo EM para estimar os parâmetros do modelo de mistura de duas distribuições Gaussianas. Hoje vamos ver o modelo de mistura com $m$ distribuições Gaussianas.
Modelo
Seja $X$ a variável de interesse. Considere que os dados possam ser originados de $m$ distribuições Gaussianas. A função de densidade do modelo é dada por
\begin{eqnarray} f(x) = \sum_{j=1}^m p_j f(x|\theta_j), \nonumber \end{eqnarray}em que $\theta_j = (\mu_j,\sigma^2_j)$ e $p_j$ são os parâmetros e o peso da $j$-ésima distribuição, respectivamente. Considerando $Y_i$ como a variável que indica a que distribuição $X_i$ pertence e dada uma amostra aleatória, a função de log-verossimilhança do modelo completo será
\begin{eqnarray} l(\theta) = \log \prod_{i=1}^n f(x_i,y_i) = \sum_{i=1}^n \sum_{y_i \in C} 1\{y_i = c\} \big[ \log(p_{y_i}) + \log(f(x_i|\theta_{y_i})) \big], \nonumber \end{eqnarray}em que $C = \{1,2,...,m\}$.
Algoritmo EM
Passo E
A função $Q$ será dada por
\begin{eqnarray} Q(\theta|\theta^{(k)}) = \sum_{i=1}^n \sum_{y_i \in C} \gamma_{ic} \big[ \log(p_{y_i}) + \log(f(x_i|\theta_{y_i})) \big], \nonumber \end{eqnarray}em que
\begin{eqnarray} \gamma_{ic} = E[1\{y_i = c\}|x_i,\theta^{(k)}] = P(Y_i = c | x_i) = \dfrac{p_c f(x_i|\theta_c)}{\sum_{j=1}^m p_j f(x_i|\theta_j)}. \nonumber \end{eqnarray}Passo M
Maximizando a função $Q$, encontramos os seguintes estimadores para os parâmetros:
\begin{eqnarray} \hat{\mu}_j &=& \dfrac{\sum_{i=1}^n (\gamma_{ij}x_i)}{\sum_{i=1}^n \gamma_{ij}}, \nonumber \\ \hat{\sigma}^2_j &=& \dfrac{\sum_{i=1}^n \gamma_{ij}(x_i-\mu_i)^2}{\sum_{i=1}^n \gamma_{ij}}, \nonumber \\ \hat{p}_j &=& (1-\sum_{k=1,k\neq j}^{m-1}p_k)\dfrac{\sum_{i=1}^n \gamma_{ij}}{\sum_{i=1}^n (\gamma_{ij}+\gamma_{im})}, \nonumber \\ \hat{p}_m &=& 1 - \hat{p}_1 - \hat{p}_2 -...-\hat{p}_{m-1}. \nonumber \end{eqnarray}Implementando o algoritmo
Agora, vamos implementar um algoritmo que recebe do usuário os dados, o número de distribuições Gaussianas que será assumido, o vetor de valores iniciais para os parâmetros, o número máximo de iterações e o critério de parada do algoritmo EM (diferença máxima permitida entre duas estimações). Para isso, vamos assumir que o vetor de parâmetros possui o seguinte padrão: $\theta = (\mu_1,...,\mu_m,\sigma^2_1,...,\sigma^2_m,p_1,...,p_{m-1})$. Perceba que o tamanho do vetor $\theta$ deve ser $3m-1$.
Abaixo mostro como fica o algoritmo. Como fizemos passo a passo a implementação para duas distribuições no post anterior, explicarei apenas as principais mudanças.
set.seed(7)
GMM_EM = function(x,m,theta_ini,max_ite=100,dif_parada=10^-3){
npar = length(theta_ini);
n = length(x)
if(length(theta_ini)!=(3*m-1)){
cat("Tamanho do vetor de valores iniciais deve ser 3m -1, em que m é o
número de distribuições consideradas.\n");
return();
}
gamaic = matrix(nrow=n,ncol=m);
theta.curr = theta_ini;
theta.trace = matrix(nrow=1,ncol=length(theta.curr));
theta.trace[1,] = theta.curr;
mu.hat = matrix(nrow=1,ncol=m);
sigma2.hat = matrix(nrow=1,ncol=m);
p.hat = matrix(nrow=1,ncol=(m-1));
indm = 1;
inds = m+1;
indp = 2*m+1;
atingiu_maxit = TRUE;
parada = matrix(0,ncol=npar,nrow=1); #menor que o erro
for(cont in 1:max_ite){
#PASSO E - CALCULO DE GAMMAIC
pm = 1 - sum(theta.curr[indp:(3*m-1)])
for(i in 1:n){
d = matrix(nrow=1,ncol=m);
for(j in 0:(m-2)){
d[1,(j+1)] = theta.curr[indp+j]*dnorm(x[i],mean=theta.curr[indm+j],
sd=sqrt(theta.curr[inds+j]));
}
d[1,m] = pm*dnorm(x[i],mean=theta.curr[m],sd=sqrt(theta.curr[2*m]));
denom = sum(d);
for(j in 1:m) gamaic[i,j] = d[1,j]/denom;
}
#PASSO M - ESTIMACAO
for(j in 1:m){
sg = sum(gamaic[,j]);
mu.hat[1,j] = sum(gamaic[,j]*x)/sg;
delta = (x-mu.hat[1,j])^2;
sigma2.hat[1,j] = sum(gamaic[,j]*delta)/sg;
}
sgm = sum(gamaic[,m]);
aux = theta.curr[indp:(3*m-1)];
for(j in 1:(m-1)){
sp = 1 - sum(aux[-j]);
sg = sum(gamaic[,j]);
p.hat[1,j] = sp* sg/(sg+sgm);
}
theta.curr = c(mu.hat[1,],sigma2.hat[1,],p.hat[1,]);
theta.trace = rbind(theta.trace,theta.curr);
dif = abs(theta.trace[cont+1,]-theta.trace[cont,])
for(j in 1:npar) {
if(dif[j] < dif_parada) {
parada[j] = 1;
}else{
parada[j] = 0;
}
}
if(sum(parada)==npar) {
cat("Algoritmo convergiu com",cont,"iterações.\n")
atingiu_maxit=FALSE;
break;
}
}
if(atingiu_maxit==T) cat("Algoritmo atingiu número máximo de iterações.\n")
return(theta.trace);
}
Vamos às principais alterações:
- Verificamos se o tamanho do vetor de valores iniciais corresponde ao número de distribuições informado.
if(length(theta_ini)!=(3*m-1)){
cat("Tamanho do vetor de valores iniciais deve ser 3m -1, em que m é o
número de distribuições consideradas.\n");
return();
}
- Como os parâmetros estão em apenas um vetor (theta.curr), armazenamos as posições do vetor em que cada conjunto de parâmetros começa, isto é, os parâmetros de média começam em [1], os de variância em [m+1] e os de peso em [2*m+1].
indm = 1;
inds = m+1;
indp = 2*m+1;
- Os passos E e M condizem com as fórmulas do começo do post. Deixo para você interpretá-las.
- A parada do algoritmo ocorre quando a diferença da estimação de cada parâmetro entre a iteração atual e a anterior é menor que o critério fornecido (dif_parada).
dif = abs(theta.trace[cont+1,]-theta.trace[cont,])
print(round(dif,4));
for(j in 1:npar) {
if(dif[j] < dif_parada) {
parada[j] = 1;
}else{
parada[j] = 0;
}
}
if(sum(parada)==npar) {
cat("Algoritmo convergiu com",cont,"iterações.\n")
atingiu_maxit=FALSE;
break;
}
Vamos testar o algoritmo acima com os mesmos dados do post anterior: duas distribuições.
set.seed(7)
x = c(rnorm(50,mean=-2,sd=1),rnorm(50,mean=2,sd=1))
theta_ini = c(-1,1,10,1,.2);
max_ite = 100;
m=2;
> res = GMM_EM(x,m,theta_ini,max_ite,dif_parada = 10^-4);
Algoritmo convergiu com 20 iterações.
Perceba que o algoritmo convergiu em um número de iterações bem menor que o máximo fornecido. Utilizar critério de parada pode nos ajudar a poupar tempo, tanto computacional quanto nosso próprio tempo. Lembre-se disso!
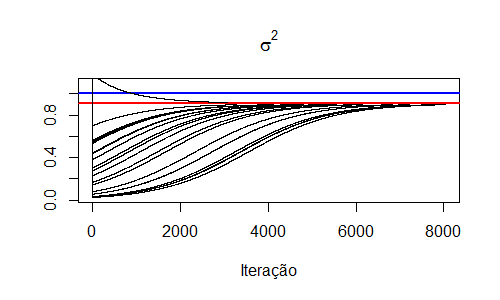
O gráfico abaixo apresenta a trajetória das estimativas dos parâmetros. Como utilizamos os mesmos valores iniciais do post anterior, obtemos o mesmo gráfico. Porém, agora com menos iterações devido ao critério de parada.
Note que, nesse caso, sabemos exatamente de quantas distribuições os dados foram originados. Suponha agora que não sabemos e informamos o número "errado" de distribuições. O que aconteceria? Vamos testar:
theta_ini = c(-1,1,5,10,1,3,.5,.1);
max_ite = 500;
m=3;
> res = GMM_EM(x,m,theta_ini,max_ite,dif_parada = 10^-4);
Algoritmo convergiu com 488 iterações.
Observe que, dessa vez, o algoritmo demorou mais para convergir. O resultado é apresentado abaixo:
> res[489,] #mu1 mu2 mu3 sigma2.1 sigma2.2 sigma2.3 p1 p2
[1] -1.99194446 1.74776537 2.45300571 0.61822279 1.20592365 0.06526058
[7] 0.44328369 0.48841668
> 1-res[489,7]-res[489,8] #p3
theta.curr
0.06829962
Note que, apesar de o algoritmo encontrar uma terceira distribuição com média 2.45, o peso dessa distribuição é bem próximo de zero. Isso indica que, apesar de assumirmos que há três distribuições, apenas duas são relevantes com mais de 90% de peso. Essas duas distribuições são bem próximas das que geramos os dados, ou seja, temos uma boa estimativa mesmo considerando três distribuições.
Agora temos um algoritmo para estimar os parâmetros do modelo de mistura de normais para um número genérico de distribuições. Incrível, não?
Espero que tenha gostado da aula.
Até a próxima aula!